Data-driven h2 model reduction for linear discrete-time systems

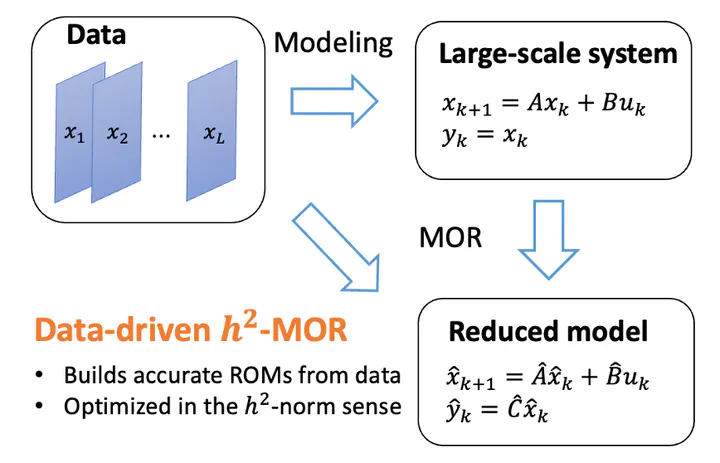
We present a new framework of h2 optimal model reduction for linear discrete-time systems. Our main contribution is to create optimal reduced-order models in the h2-norm sense directly from the measurement data alone, without using the information of the original system. In particular, we focus on the fact that the gradient of the h2 model reduction problem is expressed using the discrete-time Lyapunov equation and the discrete-time Sylvester equation, and derive the data-driven gradient. In the proposed algorithm, the initial point can be chosen as the output of the existing data-driven methods. In numerical experiments, we demonstrate that, for a modeling task in neuroscience, our method constructs a reduced-order model that outperforms DMDc in terms of the h2-norm.

conditionally accepted for publication in IEEE Transactions on Automatic Control